You are in a rowing boat on a lake. A large heavy rock is also in the boat. You heave the rock overboard. It sinks to the bottom of the lake. What happens to the water level in the lake? Does it rise, fall or stay the same?

Mechanical Engineering General ME Questions
1

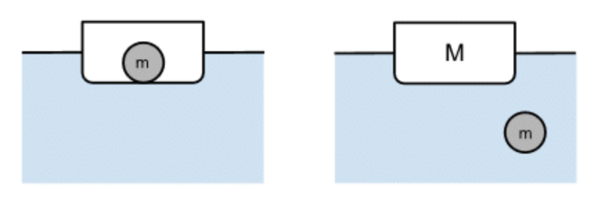
Archimede's Principle, Synapse PD, Apple

2

The mass of the boat is M and the mass of the rock is m. The density of water is Ļ_w and the density of the rock is Ļ_r.

When the rock is in the bock, Archimedeā€™s Principle is the following case:

V_{d1} = \frac{(M + m)}{Ļ_w}

When the rock is at the bottom of the lake, Archimedeā€™s Principle gives us this case:

V_{d2} = \frac{M}{Ļ_w} + \frac{m}{Ļ_r}

If you take the difference of the two, you get:

V_{d1} - V_{d2} = \frac{m}{Ļ_w} - \frac{m}{Ļ_r}

The density of the rock is greater than the density of the water, making the above equation positive. This means that more water is displaced with V_{d1}. The water level falls when the rock is thrown overboard.

1 Like