Hint: Mechanics of Materials
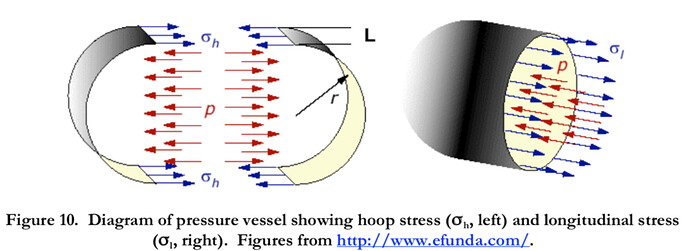
If you assume a thin wall pressure vessel, rho_long = pr/2t while rho_hoop = pr/t. Since hoop stress is twice as large as longitudinal stress, the hose will tear axially.
As @Dexter_Kenta_Yanagis mentions, this problem disguises a garden hose as a thin-walled pressure vessel, which is commonly covered in Mechanics of Materials courses.
In a cylindrical vessel with Pressure P, there are 2 stresses to consider: hoop stress trying to pull the cylinder apart radially, and longitudinal (axial) stress trying to pull the cylinder apart axially.
A visual representation of the hose as a thin-walled pressure vessel is shown here, where you can see the directions in which hoop and longitudinal stress act.
The equations for the two stresses are:
where P = pressure, R = radius of the cylinder, & T = thickness
Since the hoop stress is twice of the longitudinal stress, the hose will tear axially. Think of a hotdog cracking along the longitudinal direction first (i.e. skin fails from hoop stress generated by internal pressure!)