What are some potential sources of experimental error? How would you elimate some of these?
When designing packaging, especially for food products that need freezing or chilling, understanding how heat moves through corrugated fiberboard is crucial. For products like butter and meat that are packaged before being chilled or frozen, using packaging with high resistance can increase freezing time by up to 25%!
This experiment follows the method outlined in a study on the thermal analysis of corrugated cardboard.
Experimental Setup:
- Sample Preparation:
- Cut corrugated cardboard samples to fit the setup (e.g., 100 x 100 mm).
- Insulation Setup:
- Insulate a Tylose block on all sides except one with polystyrene sheets.
- Tylose is used in this setup because it has well-known and consistent thermal properties, such as thermal conductivity, density, and specific heat capacity, ideal for controlled experiments.
- Equilibrate the Tylose block to around 5 °C.
- Heat Source:
- Use a water bath set at 40 °C with a thin stainless steel plate on top as the isothermal surface.
- Assembly:
- Place the corrugated cardboard on the steel plate.
- Position the uninsulated side of the Tylose block on top of the cardboard.
- Apply a weight to ensure good contact between the Tylose block and the cardboard.
- Temperature Measurement:
- Embed thermocouples at the interface between the Tylose block and the cardboard, and on the opposite side.
- Connect the thermocouples to a data logger to monitor temperature changes.
Procedure:
- Allow the system to reach a steady-state temperature gradient across the cardboard.
- Record temperatures at regular intervals until the gradient stabilizes.
Data Analysis:
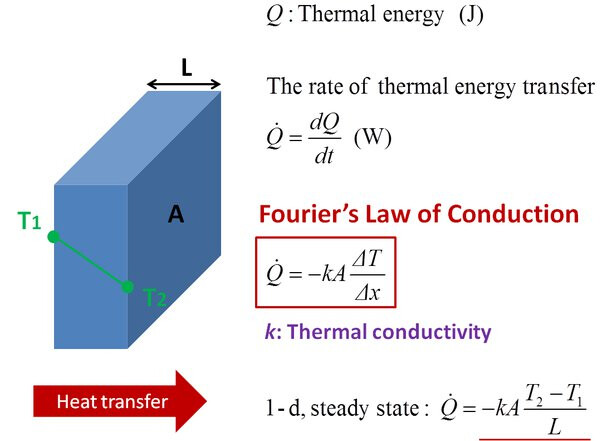
The thermal conductivity of the corrugated cardboard k_c can be calculated using the equation:
k_c = \frac{k_T x_c T}{\rho_T c_T t} \times \left(\frac{1}{Y_s^2} - \frac{1}{2} + \ln(Y_s)\right)
where k_T is the thermal conductivity of the Tylose block, x_c is the thickness of the corrugated cardboard, \rho_T is the density of the Tylose block, c_T is the specific heat capacity of the Tylose block, t is the time, and Y_s is the fraction of unaccomplished temperature change, calculated as:
Y_s = \frac{T_s - T_\infty}{T_i - T_\infty}
Validation:
- Compare the results with known values or perform repeated trials for consistency.
- Validate the results using a finite element model if available, to ensure accuracy.

