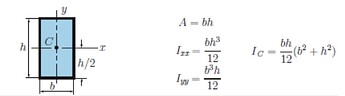The deflection of a cantilevered beam depends on four factors: load, length, material of beam, and cross-sectional shape.
- Load: How much force is applied? This can be in the form of multiple point or distributed loads applied (P)
- Length: Length of the beam (L)
- Material: Represents the modulus of elasticity - a unit of measurement of an object’s resistance to elastic (non-permanent) deformation (E)
- Cross-Sectional Shape: Represents the area moment of inertia - a geometrical propery of a cross-section that reflects how its area is distributed about a certain axis (I)
General Form:
Deflection = \frac{PL}{EI}
By looking at the equation, you can manipulate each variable in the numerator & denominator to reduce deflection:
- Reduce the load (P)
- Decrease the overall length (L)
- Material selection through using materials with a higher modulus of elasticity (E), like steel or composites that are stiffer.
- Change the cross-sectional shape (i.e. rectangle or I-beam if applied load induces bending moment and shear stresses) (I)
- Increase the beam depth - area moment of inertia of the beam’s cross-section is proportional to the cube of the depth.
- For cantilever beams, add structural reinforcements like braces/trusses.