This is a seemingly simple question imo, but can get complicated. There’s probably several good avenues to take as long as you touch on FBD and dynamics concepts but here’s one thought process:
Given:
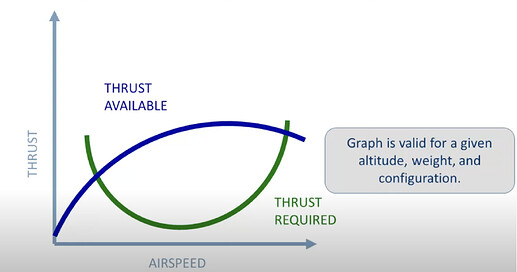
You’re given a thrust curve and basic information on an aircraft as followed for example: (Thrust Available is thrust via propellor and Thrust Required is total drag)
Source
Background:
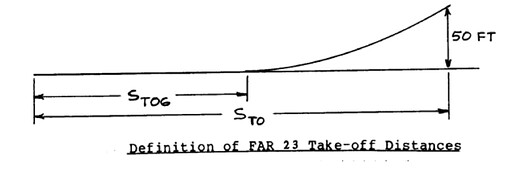
Takeoff distance is the horizontal distance an aircraft needs to reach a height of 50 feet.
Source
FBD:
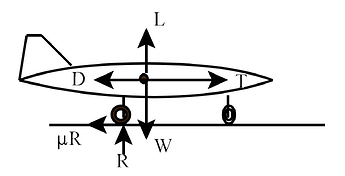
The primary forces are Lift (function of velocity), Normal (<=weight), Thrust (from curve), Drag (from curve), and Weight (constant):
Source
We’ll neglect rolling friction in this case and assume the airplane remains relatively horizontal during this process.
I’d start by splitting the two distances between on ground vs in air with different conditions.
On ground (L=0 to L=W):
Let’s start with initial v0 = 0 (velocity) and v1 is when L (lift) equals the W (weight)
W = 0.5 * Coeff. * Density * (v1)^2 * Surface Area
Assuming we’re given everything except for v1, we can get an answer for v1. Now we need to know what (t0=0s) t1 is so we can find the elapsed time and distance. Let’s start with EoM in X direction:
Thrust - Drag = F(v) = m * a
Thrust and Drag are given in the curve as a function of velocity. It you know the equations, you can subtract the two or can approximate them (some form of C(v-a)^2+b perhaps) and get a function of force in terms of v. So:
a = dv / dt = F(v) / m
It’s probably not expected to solve a diff eq. on the spot but the result will yield some function of V in terms of time
For ex. if were to be F(v) = (v+b)^2 then v(t)=1/(1/b - t/m) - b
Since you already know v1, then you can solve for t1. Then, integrate v(t) from 0s to t1 to give the total distance for this part, x1
In air (N=0, y = 0 to y=50 feet):
For this part, now that the aircraft is off the ground, N=0 and we can have an EoM for the y-component: (The v(t) previously found is in x direction and will remain so if we assume the aircraft stays roughly horizontal)
ay(t) = (L - W) / m = (Coeff. * Density * v(t)^2 * Surface Area) / 2m - gravity
We can integrate this function twice with respect to time to get some function of vertical distance in terms of time:
y(t) = F(v(t)) = 50 feet
This integral would be from t1 (not t0) to a new time, t2, and by setting it equal to 50 feet we can solve for t2 and then integrate v(t) again from t1 to t2 and get the distance for this part, x2
Final:
Now we can add x1 and x2 to get the total takeoff distance. This could probably also be solved using numerical methods, etc. but I think the main takeaway is being able to convert between different pieces of information (Force vs. Velocity chart ↔ FBD ↔ Kinematics ↔ Conditions at each stage) rather than the actual math involved.
Typical runways are a few kilometers long so an answer could fall around this range if you’re given numbers.