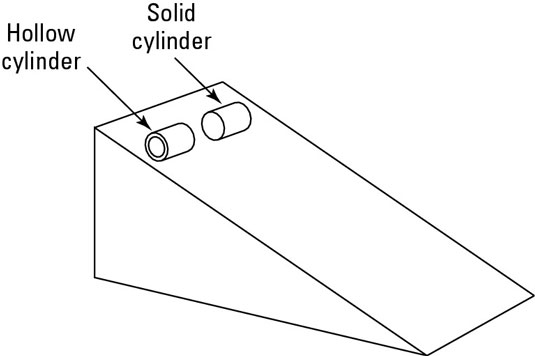
When an object is rolling down a ramp, its energy is made up of three components:
𝑚𝑔ℎ=1/2𝑚𝑣^2+12𝐼𝜔^2
The first term is the potential energy; this is the energy is takes to lift the object up the ramp. This is equal to 𝑚𝑔ℎ with 𝑚m being the mass, 𝑔 the acceleration due to gravity, and ℎ the height of the ramp.
The second term is the translational kinetic energy; this is the energy it takes for the object to move down the ramp.
The third term is the rotational kinetic energy; this is the energy it takes for the object to roll. This is equal to 1/2𝐼𝜔^2, with 𝐼 being the moment of inertia (the object’s resistance to being rotated) and 𝜔 being the angular velocity.
For the hollow cylinder, the mass is placed the farthest from the center and thus 𝑟 is large, 𝐼 is large, and consequently it is slow. For the case of the solid cylinder, the mass distribution occurs more closer to the center, thus has lower 𝐼 and highest velocity.
Thus, the solid cylinder reaches the bottom first.
1 Like
If you want to practice more questions like this, check out these other moment of inertia problems!
Here are some other tricky questions:
I think they should reach the bottom at the same time
Hi @Shan_L.Wang , this article helps explain why the solid rod reaches the bottom first! In the case of if they’re sliding (i.e. not rolling) then yes they would reach the bottom at the same time. You would not need to factor the moment of inertia in the case of a sliding rod.
Article Link: Rolling Race - Scientific American.
You should find that a solid object will always roll down the ramp faster than a hollow object of the same shape (sphere or cylinder)—regardless of their exact mass or diameter. This might come as a surprising or counterintuitive result! A classic physics textbook version of this problem asks what will happen if you roll two cylinders of the same mass and diameter—one solid and one hollow—down a ramp. The answer is that the solid one will reach the bottom first. In that specific case it is true the solid cylinder has a lower moment of inertia than the hollow one does. (Although they have the same mass, all the hollow cylinder’s mass is concentrated around its outer edge so its moment of inertia is higher.)
But it is incorrect to say “the object with a lower moment of inertia will always roll down the ramp faster.” It takes a bit of algebra to prove (see the “Hyperphysics” link below), but it turns out that the absolute mass and diameter of the cylinder do not matter when calculating how fast it will move down the ramp—only whether it is hollow or solid. So, in this activity you will find that a full can of beans rolls down the ramp faster than an empty can—even though it has a higher moment of inertia. (It has the same diameter, but is much heavier than an empty aluminum can.) Applying the same concept shows two cans of different diameters should roll down the ramp at the same speed, as long as they are both either empty or full. The same principles apply to spheres as well—a solid sphere, such as a marble, should roll faster than a hollow sphere, such as an air-filled ball, regardless of their respective diameters.
Cool animation from Wikipedia