Sampling rates are especially important for converting analog to digital signals.
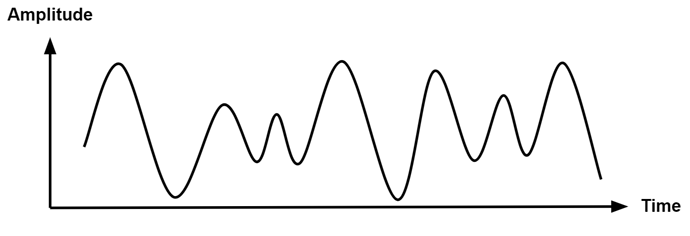
Analog signals, akin to continuous values over time, surround us in many forms. When you think of microphones, resistive touch screens, force sensors, etc., these are all analog signals. When plotted on curves, analog signals produce a smooth, continuous waveform.
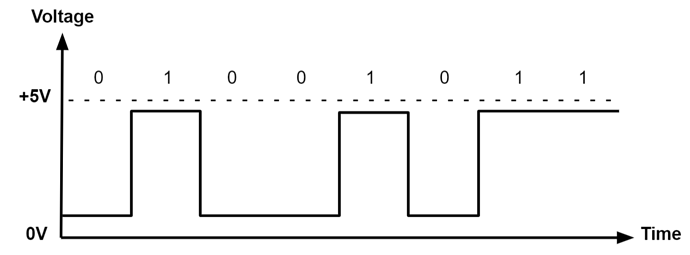
In contrast, digital signals represent data as a sequence of discrete values, and can only take on one value from a finite set of possible values at any given time.
All modern computers and data transmission devices use digital signals. As such, in order to replicate analog signals in the digital domain, analog-to-digital (ADC) converters are needed. This is where the important of the Nyquist Theorem comes in play:
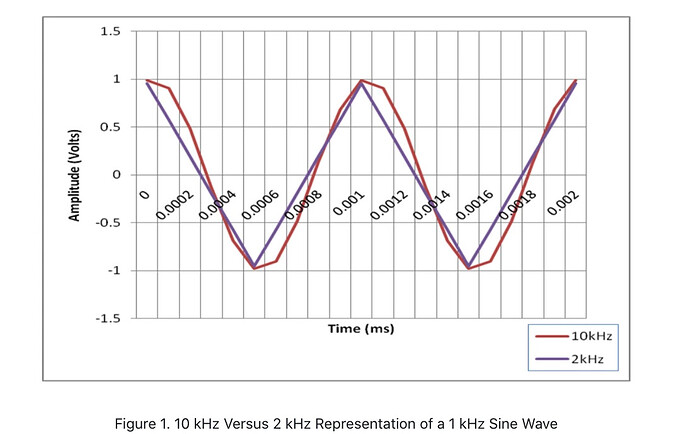
The Nyquist Theorem states that you can accurately reconstruct a signal by sampling two times the highest frequency component of interest. However, in practice, you should sample at least 10 times the maximum frequency to represent the shape of your signal.
TLDR; Sample with at least 2x the highest frequency to reconstruct a continuous function from samples
The sampling frequency or sampling rate , fs , is the average number of samples obtained in one second, thus fs = 1/T . Its units are samples per second or hertz (48 kHz is 48,000 samples per second) ’